Answer:
1) height = 15cm
2) Base Area = 80cm²
3)
 cubic kilometers
cubic kilometers
Explanation:
Let's address each part of the question:
1) Determine the height:
For the rectangle face, we can use the Pythagorean theorem since we know the diagonal (
 ) and one side (
) and one side (
 ). Let
). Let
 be the height.
be the height.

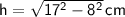
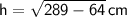
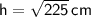
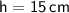
So, the height of the rectangular prism is
 .
.

2) Calculate the area of the bottom base/face:
For the bottom base, the area (
 ) is given by the product of the length and width.
) is given by the product of the length and width.
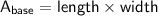
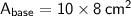
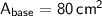
So, the area of buttom base/face = 80 cm².

3) Calculate the volume of the rectangular prism and convert to kilometers cubed:
Given that the volume (
 ) is
) is
 , to convert this volume to kilometers cubed, we divide by
, to convert this volume to kilometers cubed, we divide by
 (since there are
(since there are
 cubic centimeters in a cubic kilometer).
cubic centimeters in a cubic kilometer).
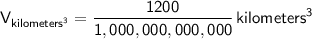
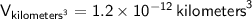
So, the rectangular prism can hold
 cubic kilometers of water.
cubic kilometers of water.