Question

The length, in millimeters of each side of a square shaped electronic chip is a rational number. What statement is true about the length of the diagonal of the chip

Answer 1

The diagonal is irrational because it is a product of a rational and an irrational number

Explanation:

The options are not given. However, the question is still answerable.

Given

Shape: Square

Length: Rational

Since the side length is said to be rational, I'll answer the question based on whether the diagonal is rational or not.

Having said that:

The diagonal (d) of a square with side length (l) is calculated using Pythagoras theorem.

`d^2 = l^2 + l^2`

`d^2 = 2l^2`

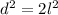
Take positive square root of both sides

`d = √(2l^2)`

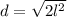
Split:

`d = √(2) * √(l^2)`

`d = √(2) *l`

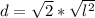
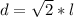
Recall that the side length (l) is rational.

However,
`\sqrt 2` is irrational.

So, the product of l and
`\sqrt 2` will be irrational

Hence:

The diagonal is irrational