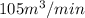Answer:
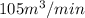
Explanation:
We are given that
Base side of square pyramid, a=3 m
Height of square pyramid, h=9m
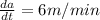
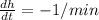
We have to find the rate of change of the volume of the pyramid at that instant.
Volume of square pyramid, V=

Differentiate w.r.t t

Substitute the values
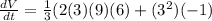
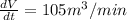
Hence, the rate of change of the volume of the pyramid at that instant=