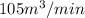Question

The side of the base of a square pyramid is increasing at a rate of 666 meters per minute and the height of the pyramid is decreasing at a rate of 111 meter per minute. At a certain instant, the base's side is 333 meters and the height is 999 meters. What is the rate of change of the volume of the pyramid at that instant (in cubic meters per minute)

Answer 1

`105m^3/min`

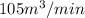
Explanation:

We are given that

Base side of square pyramid, a=3 m

Height of square pyramid, h=9m

`(da)/(dt)=6m/min`

`(dh)/(dt)=-1/min`

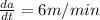
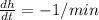
We have to find the rate of change of the volume of the pyramid at that instant.

Volume of square pyramid, V=
`(1)/(3)a^2h`

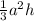
Differentiate w.r.t t

`(dV)/(dt)=(1)/(3)(2ah(da)/(dt)+a^2(dh)/(dt))`

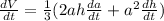
Substitute the values

`(dV)/(dt)=(1)/(3)(2(3)(9)(6)+(3^2)(-1)`

`(dV)/(dt)=105m^3/min`

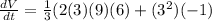
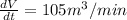
Hence, the rate of change of the volume of the pyramid at that instant=
`105m^3/min`