Question

The part is made by taking tubing of radius 1 cm and adhering a rounded coarse piece to one end of it. The rounded piece follows the curvature of a sphere of radius 3 cm. This design is modeled by the portion of the cylinder (centered around the z-axis) that is above the xy-plane and enclosed in the sphere of radius 3 centered at the origin 1) Write the equation of the sphere described above in Cartesian, cylindrical, and spherical coordinates. 2) Write the equation of the cylinder described above in Cartesian, cylindrical, and spherical coordinates. 3) The density of all of the parts combined is made to be δ(x, y, z) = z kg/cm3. Set up the triple integral to find the mass of the part, including bounds. Then evaluate the integral from the previous part to find the mass of the part. 4) Finally, find the center of mass of the part.

Answer 1

1) Sphere:
`\(x^2 + y^2 + z^2 = 9\) in Cartesian, \(r = 3\)` in cylindrical, and
`\(\rho = 3\)` in spherical coordinates.

2) Cylinder:
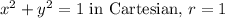`\(x^2 + y^2 = 1\) in Cartesian, \(r = 1\)` in cylindrical, and
`\(\rho = √(z^2 + 1)\)` in spherical coordinates.

3) Triple integral for mass:
`\(\int_(-1)^(1) \int_(-√(1-x^2))^(√(1-x^2)) \int_(x^2 + y^2)^(3) z \, dz \, dy \, dx\).`

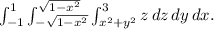
4) Center of mass:
`\((0, 0, 3/2)\).`

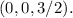
Step-by-step explanation:

The given sphere has a radius of 3 and is centered at the origin, leading to the Cartesian equation
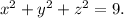`\(x^2 + y^2 + z^2 = 9\).` In cylindrical coordinates, the radius r is 3, and in spherical coordinates, the radial coordinate
`\(\rho\)`is also 3. For the cylinder, it is confined to the xy-plane with a radius of 1, resulting in
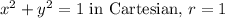`\(x^2 + y^2 = 1\) in Cartesian, \(r = 1\)` in cylindrical, and
`\(\rho = √(z^2 + 1)\)` in spherical coordinates.

To find the mass of the part, we set up a triple integral using the given density function
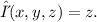`\(δ(x, y, z) = z\).` The integral bounds are determined by the region enclosed by the cylinder and sphere:
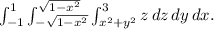`\(\int_(-1)^(1) \int_(-√(1-x^2))^(√(1-x^2)) \int_(x^2 + y^2)^(3) z \, dz \, dy \, dx\).`Finally, the center of mass is calculated to be
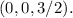`\((0, 0, 3/2)\).` This means that, on average, the mass is concentrated at a point above the xy-plane, specifically at a distance of 3/2 units along the z-axis.