Answer: 33%
===========================================================
Step-by-step explanation:
1/3 converts to the decimal form 0.333333... where the 3's go on forever
5/3 is a similar story but 5/3 = 1.666666.... where the '6's go on forever
The notation
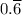 indicates that the 6's go on forever.
indicates that the 6's go on forever.
So,
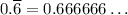
The horizontal bar tells us which digits repeat. As another example,
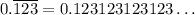
The three dots just mean "keep this pattern going forever".
----------
Everything mentioned so far has the decimal portions go on forever repeating some pattern over and over.
The only one that doesn't do this is 33% which converts to the decimal form 0.33
The value 0.33 is considered a terminating decimal since "terminate" means "stop". So this is the value that doesn't fit in with the other three items mentioned.