Answer:
Must get common denominators (explained more in explanation)
Explanation:
To add or subtract polynomials with unlike denominators, you first have to get common denominators, For example:
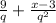
Multiply the first fraction on the left by
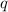 so we get:
so we get:

After this, you just have to add them
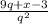
Another example is:
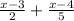
We multiply the first fraction by 5 and the second fraction by 2 through distributive property
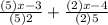
Multiply
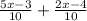
Add
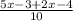
Simplify by combining like terms
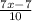
Hope this helps!