Answer:


Explanation:
To eliminate the x-terms in the system of equations
 and
and
 , we can manipulate the equations to make the coefficients of x in both equations the same or multiples of each other.
, we can manipulate the equations to make the coefficients of x in both equations the same or multiples of each other.
In this case, we want to eliminate the x-terms by making the coefficients the same.
First, let's find the least common multiple of 2 and 3, which is 6.
Multiply the first equation by 3 and the second equation by 2:
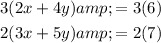
This results in the following system of equations:
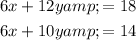
Now, the coefficients of x in both equations are the same (6).
We can subtract the second equation from the first to eliminate the x-terms:
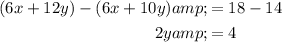
Now, we can solve for y by dividing both sides by 2:
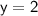
Now that we have the value for y, we can substitute it back into either of the original equations to solve for x. Let's use the first equation:
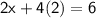
Solving for x:
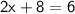
Subtracting 8 from both sides:
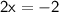
Dividing by 2:

So, the solution to the system of equations is
 and
and
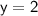 .
.
Therefore, the answer is:

