Question

Solve for xx. Round to the nearest tenth of a degree, if necessary

Answer 1

x = 55°

Explanation:

Given:

• Adjacent = OP = 5.1
• Hypotenuse = OQ = 8.9

To find:

x° = ?

Solution:

The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse of a right triangle.

`\sf cos (x) = (adjacent )/( hypotenuse)`

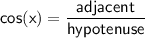
In this case, the adjacent side is 5.1 and the hypotenuse is 8.9.

Therefore, the cosine of angle x is:

`\sf cos(x) =(OP)/(OQ)\\\\ =( 5.1)/(8.9)\\\\ = 0.5730337078651`

To find the angle x in degrees, we can use the following formula:

`\sf angle( x )= cos^(-1)(cos x)`

`\sf angle( x )= cos^(-1)( 0.5730337078651 )`

`\sf angle( x ) = 55.037952471005`

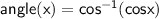
In nearest tenth

`\sf angle( x ) \approx 55.0`

Therefore, the angle x is 55°