Answer:
97.0 ft
Step-by-step explanation:
The given diagram shows two right triangles, both of which share a common height (x).
To find the height of the lighthouse (x), we can create two equations by substituting the information for each triangle into the tangent trigonometric ratio.

Triangle 1
- Angle = 30°
- x is the side opposite the angle.
- y is the side adjacent the angle.
Therefore, substituting these values into the tangent ratio gives:
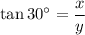
Rearrange to isolate y:
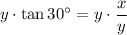
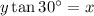
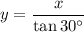
Triangle 2
- Angle = 25°
- x is the side opposite the angle.
- (y + 40) is the side adjacent the angle.
Therefore, substituting these values into the tangent ratio gives:
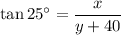
Rearrange to isolate y:
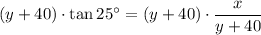
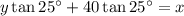

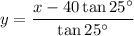
Now, we have created two equations:

Substitute the first equation into the second equation, so that we have an equation in terms of x only:
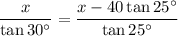
Now, solve for x:
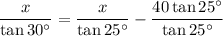

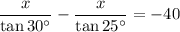
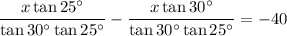
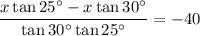
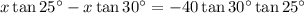
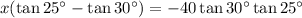
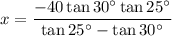
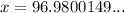
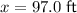
Therefore, the height of the lighthouse (x) is 97.0 ft (rounded to the nearest tenth).