Question

A 75-hp (shaft output) motor that has an efficiency of 91.0% is worn out and is replaced by a high-efficiency 75-hp motor that has an efficiency of 95.4%. Determine the reduction in the heat gain of the room due to higher efficiency under full-load conditions.

Answer 1

the reduction in the heat gain is 2.8358 kW

Step-by-step explanation:

Given that;

Shaft outpower of a motor
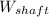`W_(shaft)` = 75 hp = ( 75 × 746 ) = 55950 W

Efficiency of motor
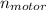`n_(motor)` = 91.0% = 0.91

High Efficiency of the motor
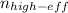`n_(high-eff)` = 95.4% = 0.954

now, we know that, efficiency of motor is defined as;
`n_(motor)` =
`W_(shaft)` /
`W_(elec)`

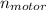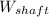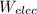
where
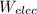`W_(elec)` is the electric input given to the motor

so

`W_(elec)` =
`W_(shaft)` /
`n_(motor)`

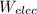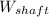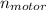
we substitute

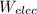`W_(elec)` = 55950 W / 0.91

= 61483.5 W

= 61.4835 kW

now, the electric input given to the motor due to increased efficiency will be;

`W_(elec-incresed)` =
`W_(shaft)` /
`n_(high-effic)`

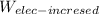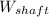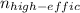
we substitute

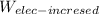`W_(elec-incresed)` = 55950 W / 0.954

= 58647.79 W

= 58.6477 kW

so the reduction of the heat gain of the room due to higher efficiency will be;

Q =
`W_(elec)` -
`W_(elec-incresed)`

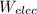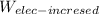
we substitute

Q = 61.4835 kW - 58.6477 kW

Q = 2.8358 kW

Therefore, the reduction in the heat gain is 2.8358 kW