The distance traveled before the speed is reduced to zero is
 . If the force continues to be applied, the speed of the box at t=3.00s is 54m/s.
. If the force continues to be applied, the speed of the box at t=3.00s is 54m/s.
To solve this problem, we can use the kinematic equations of motion and Newton's second law. Let's break it down into parts:
Part (a):
The net force acting on the box is given by Newton's second law:
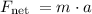
The acceleration a is the second derivative of position x with respect to time t:
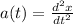
The force F(t) is given by the problem as
 . We can find acceleration by taking the derivative twice:
. We can find acceleration by taking the derivative twice:
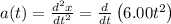
Integrate this acceleration function to get the velocity function, and then integrate the velocity function to get the position function:
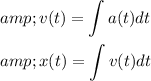
To find the distance the box moves before its speed is reduced to zero, you need to find the time t when v(t)=0. Solve for t in the velocity equation and substitute this into the position equation to find the distance.
Acceleration (a(t)):
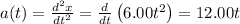
Velocity (v(t)):
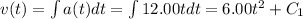
where
 is an integration constant.
is an integration constant.
Position (x(t)):
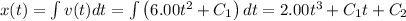
where
 and
and
 are integration constants.
are integration constants.
Now, to find the distance the box moves before its speed is reduced to zero, we set v(t)=0 and solve for t:
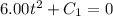
Solving for t gives t=0 (ignoring the negative solution, as we are dealing with time).
Substitute this t value into the position equation:
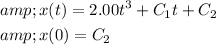
So, the distance the box moves before its speed is reduced to zero is given by
 .
.
Given
 , we know that v(0)=0 (initial speed is given as 9 m/s). Substituting t=0 into v(t), we find
, we know that v(0)=0 (initial speed is given as 9 m/s). Substituting t=0 into v(t), we find
 .
.
Now,
 . The distance before the speed is reduced to zero is given by
. The distance before the speed is reduced to zero is given by
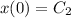 .
.
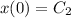
So,
 is the distance traveled before the speed is reduced to zero.
is the distance traveled before the speed is reduced to zero.

So, the distance traveled before the speed is reduced to zero is
 .
.
Part (b):
To find the speed at t=3.00s, use the velocity function v(t) that you obtained in part (a) and evaluate it at t=3.00s.
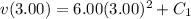

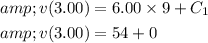
Question:
A 2.00-kg box is moving to the right with speed 9 m/s
on a horizontal, frictionless surface. At t=0 a horizontal
force is applied to the box. The force is directed to the left and
has magnitude
 .
.
(a) What distance does the box move from its position at t=0 before its speed is reduced to zero?
(b) If the force continues to be applied, what is the speed of the box at t=3.00s.