Question

A fox locates its prey under the snow by slight sounds rodents make. The fox then leaps straight into the air, and then burrows its nose into the snow to catch its meal. If a fox jumps up to a height of 79 cm, calculate (a) the speed at which the fox leaves the snow, and (b) how long the fox is in the air. Ignore air resistance.m/s:s:You throw a baseball directly upward at time t = 0 at an initial speed of 12.9 m/s. What is the maximum height the ball reaches above where it leaves your hand? At what times does the ball pass through half the maximum height? Ignore air resistance and take g = 9.80 m/s2.Maximum height:Earlier time at half maximum height:Later time at half maximum height:

Answer 1

1.a) 3.93 m/s

b) 0.80 s

2. a) 8.49 m

b) 0.39 s

Step-by-step explanation:

1. a) The speed at which the fox leaves the snow can be found as follows:

`v_(f)^(2) = v_(0)^(2) - 2gH`

Where:

g: is the gravity = 9.80 m/s²

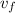`v_(f)`: is the final speed = 0 (at the maximum height)

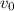`v_(0)`: is the initial speed =?

H: is the maximum height = 79 cm = 0.79 m

`v_(0) = √(2gH) = \sqrt{2*9.80 m/s^(2)*0.79 m} = 3.93 m/s`

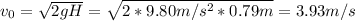
Hence, the speed at which the fox leaves the snow is 3.93 m/s.

b) The time at which the fox reaches the maximum height is given by:

`v_(f) = v_(0) - gt`

`t = (v_(0) - v_(f))/(g) = (3.93 m/s)/(9.80 m/s^(2)) = 0.40 s`

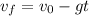
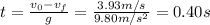
Now, the time of flight is:

`t_(v) = 2t = 2*0.40 s = 0.80 s`

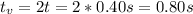
2. a) The maximum height the ball reaches is:

`H = (v_(0)^(2) - v_(f)^(2))/(2g) = ((12.9 m/s)^(2))/(2*9.80 m/s^(2)) = 8.49 m`

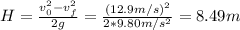
Then, the maximum height is 8.49 m.

b) The time at which the ball passes through half the maximum height is:

`y_(f) = y_(0) + v_(0)t - (1)/(2)gt^(2)`

Taking y₀ = 0 and
`y_(f)` = 8.49/2 = 4.245 m we have:

`4.245 m -12.9m/s*t + (1)/(2)*9.80m/s^(2)*t^(2) = 0`

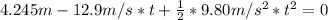
By solving the above quadratic equation we have:

t = 0.39 s

Therefore, the time at which the ball passes through half the maximum height when the ball is going up is 0.39 s.

I hope it helps you!