Answer:
(-5, -4)
Explanation:
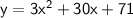
To rewrite the given quadratic equation in the form you mentioned and find the vertex (extreme value), we can complete the square as follows:
Start with the equation:
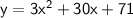
First, factor out the coefficient of x² (which is 3) from the x² and x terms:
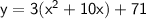
Now, to complete the square, we need to add and subtract a value that will make the expression inside the parentheses a perfect square trinomial. To do that, we take half of the coefficient of x (which is 10) and square it:

Add and subtract 25 inside the parentheses:
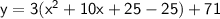
Now, factor the perfect square trinomial inside the parentheses:

Distribute the 3 to both terms inside the parentheses:

Simplify the constants:
y = 3(x + 5)^2 - 75 + 71
Combine the constants:
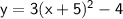
Now the equation is in the desired form:
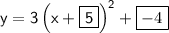
The vertex form is
 , where (h, k) is the vertex.
, where (h, k) is the vertex.
In this case,
the vertex is at the point (-5, -4).
So, the extreme value (vertex) is at (-5, -4).