Answer:
Explanation:
From the given information:
The uniform distribution can be represented by:
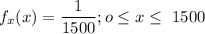
The function of the insurance is:
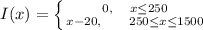
Hence, the variance of the insurance can also be an account forum.
![Var [I_((x)) = E [I^2(x)] - [E(I(x)]^2](https://img.qammunity.org/2022/formulas/mathematics/college/mtr9acplg6y6zmrc87acqrd36vy0bkoiv6.png)
here;
![E[I(x)] = \int f_x(x) I (x) \ sx](https://img.qammunity.org/2022/formulas/mathematics/college/3zavvy39jn26yoeybaashexb1jqi1vqrwf.png)
![E[I(x)] = (1)/(1500) \int ^(1500)_{250{ (x- 250) \ dx](https://img.qammunity.org/2022/formulas/mathematics/college/8whevxz0250kn5qjl09va2p1fdelmfyohx.png)

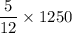
Similarly;
![E[I^2(x)] = \int f_x(x) I^2 (x) \ sx](https://img.qammunity.org/2022/formulas/mathematics/college/vx0rtkuzo82s1pwdum2e0gle9vq6g15ghi.png)
![E[I(x)] = (1)/(1500) \int ^(1500)_{250{ (x- 250)^2 \ dx](https://img.qammunity.org/2022/formulas/mathematics/college/avkosqtog5lrk7k9d4a93vqry5tmm73skt.png)

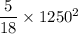
∴
![Var {I(x)} = 1250^2 \Big [ (5)/(18) - (25)/(144)]](https://img.qammunity.org/2022/formulas/mathematics/college/oxyxo5iksa4pnp5vl1uqtr6vw0v26yd94f.png)
Finally, the standard deviation of the insurance payment is:
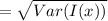
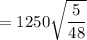
≅ 404