Answer:
6.132 meters
Step-by-step explanation:
To solve this problem, we can use the following steps:
1. Identify the known and unknown quantities.
Known quantities:
- Horizontal velocity of the water balloon, u = 6.35 m/s
- Width of the alley, w = 7.1 m
Unknown quantity:
- Maximum distance the water balloon can fall, h
2. Choose the appropriate equation of motion.
Since the water balloon is moving horizontally in free fall, we can use the following equation of motion:
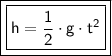
where:
- h is the distance fallen
- g is the acceleration due to gravity (9.81 m/s^2)
- t is the time taken to fall
3. Solve for the unknown quantity.
We can rearrange the equation to solve for h:
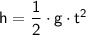
To find t, we can use the following equation of motion for horizontal motion:

where:
- w is the distance traveled
- u is the initial velocity
- t is the time taken to travel the distance
Substituting in the known values, we get:
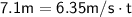
Solving for t, we get:
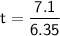

Substituting this value back into the equation for h, we get:
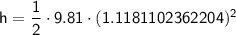

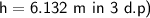
Therefore, Ms. Burns' enemy can be up to 6.132 meters below her and she will still hit them with the water balloon.