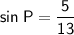Answer:
Explanation:
Given:
In ∆ PQR
To find:
Solution:
To find sin P, we can use the following formula:

We know that QR = 5 and that PR = the hypotenuse of the triangle. We can use the Pythagorean Theorem to find PR:
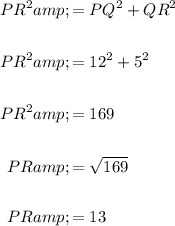
Now that we know the values of QR and PR, we can plug them into the formula for sin P:
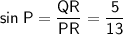
Therefore,