Question

Lim x tends to 2. Evaluate x^2 -4 /x-2

Answer 1

4

Explanation:

`\lim_(x \to \22) ((x^2-4)/(x-2) )`
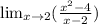
If you solve by substituting 2 into the function, you get indeterminate form where the limit of the numerator and denominator are both 0. Instead, you can factor the numerator

`\lim_(x \to \22)(x^2-4)/(x-2) = \lim_(x \to \22)((x+2)(x-2))/(x-2)`
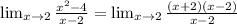
From here, you can "cancel out" the (x-2) term and you are left with

`\lim_(x \to \22) (x+2)`
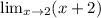
Substitute 2 for x, and you get 2 + 2 = 4.