Question

HELP! Question is attached bellow

Answer 1

Up- Right Graph

Explanation:

`\sf ((y+1)^2)/(9) - ((x-2)^2)/(16) = 1`

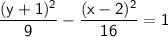
The given equation represents a hyperbola in standard form.

we can find the graph by knowing the center, foci and vertices and we need to compare it to the general equation for a hyperbola with a horizontal major axis:

`\sf ((y - k)^2)/(a^2) - ((x - h)^2)/(b^2) = 1`

In this case, we have:

`\sf ((y + 1)^2)/(9) - ((x - 2)^2)/(16) = 1`

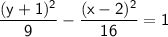
We can see that the center of the hyperbola is at the point (h, k), which is (2, -1) in this case.

Now, let's find the values of a and b:

a² = 9, so a = 3

b²= 16, so b = 4

The value of c (the distance from the center to the foci) can be found using the relationship:

`\sf c^2 = a^2 + b^2`

`\sf c^2 = 3^2 + 4^2`

`\sf c^2 = 9 + 16`

`c^2 = 25`

`c =√(25)`

`c = 5`

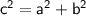
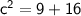
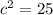
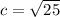
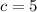
So, the distance from the center to the foci is 5 units. To find the foci, we can add and subtract c to the x-coordinate of the center:

Foci:

1. (2 + 5, -1) = (7, -1)

2. (2 - 5, -1) = (-3, -1)

So, the coordinates of the foci are (7, -1) and (-3, -1).

To find the vertices, you can add and subtract to the y-coordinate of the center:

Vertices:

1. (2, -1 + 3) = (2, 2)

2. (2, -1 - 3) = (2, -4)

So, the coordinates of the vertices are (2, 2) and (2, -4).

In summary:

Center: (2, -1)

Foci: (7, -1) and (-3, -1)

Vertices: (2, 2) and (2, -4)

In the figure,

The vertices (2, 2) and (2, -4) are matched up to the Up- Right graph.

So, the answer is Up-Right graph.