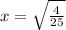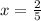Answer:
(a)
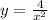
(b)
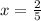
Explanation:
Given
Variation: Inverse proportional.
This is represented as:
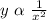
See attachment for table
Solving (a):
First convert variation to equation
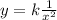
From the table:
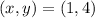
So, we have:
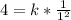
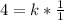

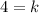
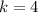
Substitute 4 for k in
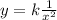
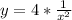
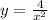
Solving (b): x when y = 25.
Substitute 25 for y in
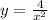
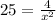
Cross Multiply
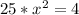
Divide through by 25
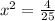
Take positive square roots of both sides