Question

Five-foot-tall Melody casts an 84-inch shadow. How tall is her friend if, at the same time of day, his shadow is 1 foot shorter than hers?

Answer 1

The height of her friend is 4.826 feet.

Explanation:

The length of the shadow (
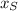`x_(S)`), measured in feet, is directly proportional to the height of the person (
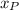`x_(P)`), measured in feet. That is:

`x_(P) \propto x_(S)`

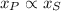
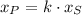`x_(P) = k\cdot x_(S)` (1)

Where
`k` is the proportionality constant, no unit.

We can eliminate this constant by constructing this relationship:

`(x_(P,M))/(x_(S,M)) = (x_(P,F))/(x_(S,F))` (2)

Where M and F represents Melody and Melody's friend. If we know that
`x_(P,M) = 5\,ft`,
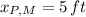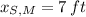`x_(S,M) = 7\,ft` and
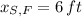`x_(S,F) = 6\,ft`, then the height of his friend is:

`x_(P,F) = \left((x_(P,M))/(x_(S,M)) \right)\cdot x_(S,F)`

`x_(P,F) = \left((5\,ft)/(7\,ft)\right)\cdot (6\,ft)`

`x_(P,F) = 4.286\,ft`

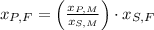
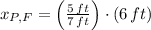
The height of her friend is 4.826 feet.