Given:
The polynomial is
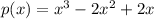
To find:
The real and complex zeros of the equation.
Solution:
We have,
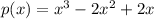
For zeros, p(x)=0.
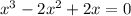
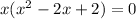
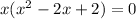
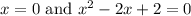
The real value of x is 0. The equation
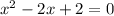 will give complex roots. Here, a=1, b=-2 and c=2.
will give complex roots. Here, a=1, b=-2 and c=2.
Using quadratic formula, we get




On further simplification, we get

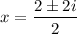
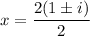
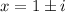
Therefore, the real zero is 0 and the complex zeros are 1+i and 1-i.