Question

P(x) = x3 - 2x2 + 2x
What are the real and complex zeros of the equation

Answer 1

Given:

The polynomial is

`p(x)=x^3-2x^2+2x`

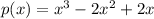
To find:

The real and complex zeros of the equation.

Solution:

We have,

`p(x)=x^3-2x^2+2x`

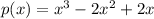
For zeros, p(x)=0.

`x^3-2x^2+2x=0`

`x(x^2-2x+2)=0`

`x(x^2-2x+2)=0`

`x=0\text{ and }x^2-2x+2=0`

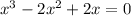
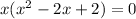
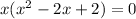
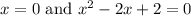
The real value of x is 0. The equation
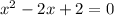`x^2-2x+2=0` will give complex roots. Here, a=1, b=-2 and c=2.

Using quadratic formula, we get

`x=(-b\pm √(b^2-4ac))/(2a)`

`x=(-(-2)\pm √((-2)^2-4(1)(2)))/(2(1))`

`x=(2\pm √(4-8))/(2)`

`x=(2\pm √(-4))/(2)`

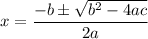
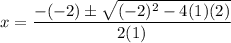
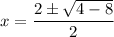
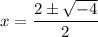
On further simplification, we get

`x=(2\pm √(-1)√(4))/(2)`

`x=(2\pm 2i)/(2)`

`x=(2(1\pm i))/(2)`

`x=1\pm i`

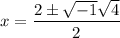
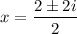
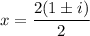
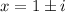
Therefore, the real zero is 0 and the complex zeros are 1+i and 1-i.