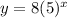Answer:
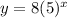
Explanation:
We want an exponential function that goes through the two points (0, 8) and (2, 200).
Since a point is (0, 8), this means that y = 8 when x = 0. Therefore:

Simplify:
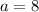
So we now have:
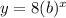
Likewise, the point (2, 200) tells us that y = 200 when x = 2. Therefore:

Solve for b. Dividing both sides by 8 yields:
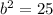
Thus:
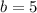
Hence, our exponential function is: