Answer:

Explanation:
Given
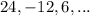
Required
Write a formula
The above sequence shows a geometric sequence because:
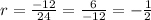 -- common ratio
-- common ratio
The equation is determined using:
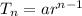
Where
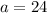
Substitute values for a and r
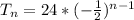
Apply law of indices:


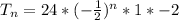
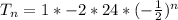

The above represents the explicit formula