Question

Write an explicit formula for the An, and the n^th term of the sequence 24,-12,6,....

Answer 1

`T_n = -48* (-(1)/(2))^(n)`

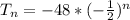
Explanation:

Given

`24, -12, 6,...`

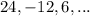
Required

Write a formula

The above sequence shows a geometric sequence because:

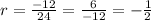`r = (-12)/(24) = (6)/(-12) = -(1)/(2)` -- common ratio

The equation is determined using:

`T_n = ar^(n-1)`

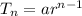
Where

`a = 24`

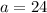
Substitute values for a and r

`T_n = 24* (-(1)/(2))^(n-1)`

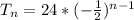
Apply law of indices:

`T_n = 24* (-(1)/(2))^(n) * (-(1)/(2))^(-1)`

`T_n = 24* (-(1)/(2))^(n) * 1/(-(1)/(2))`

`T_n = 24* (-(1)/(2))^(n) * 1*-2`

`T_n = 1*-2*24* (-(1)/(2))^(n)`

`T_n = -48* (-(1)/(2))^(n)`

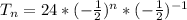
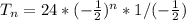
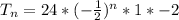
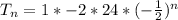
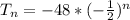
The above represents the explicit formula