Answer:
-2
Explanation:
The first negative term in the sequence is the first term that is less than zero. This means that we need to find the value of n for which T(n) < 0.
We can start by setting T(n) = 0 and solving for $n$:
46 - 4n = 0
-4n = -46
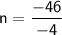
n = 11.5
Since ln must be an integer, the first negative term in the sequence is for n = 12.
To find the value of the first negative term, we can simply substitute n = 12 into the formula for T(n):
T(12) = 46 - 4(12)
T(12) = 46 - 48
T(12) = -2
Therefore, the value of the first negative term in the sequence is -2.