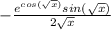Question

F(x) = e^(cos √x) find f'(x)​

Answer 1

`-(e^(cos(√(x) ))sin(√(x) ) )/(2√(x) )`

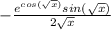
Explanation:

use chain rule

c(x)= e^x

c'(x) = e^x

g(x) = cos(
`√(x)`)

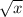g'(x) = 
`(-sin(√(x) ))/(2√(x) )`

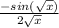
(use the chain rule again, to solve for g'(x))

h(x) = cos(x)

h'(x) = -sin(x)

j(x) =
`√(x)`

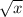
j'(x) =
`(1)/(2√(x) )`

g'(x) = h'(j(x)) * j'(x)

g'(x) = -sin(
`√(x)`) *
`(1)/(2√(x) )` =
`(-sin(√(x) ))/(2√(x) )`

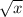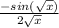
Let's do the first expression using the chain, since now we now the value of g'(x)

f'(x) = c'(g(x))*g'(x)

f'(x) =
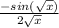`e^(cos(√(x) ))` *
`(-sin(√(x) ))/(2√(x) )` =
`-(e^(cos(√(x) ))sin(√(x) ) )/(2√(x) )`