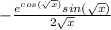Answer:
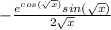
Explanation:
use chain rule
c(x)= e^x
c'(x) = e^x
g(x) = cos(
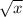 )
)
g'(x) =
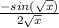
(use the chain rule again, to solve for g'(x))
h(x) = cos(x)
h'(x) = -sin(x)
j(x) =
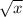
j'(x) =
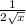
g'(x) = h'(j(x)) * j'(x)
g'(x) = -sin(
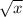 ) *
) *
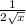 =
=
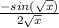
Let's do the first expression using the chain, since now we now the value of g'(x)
f'(x) = c'(g(x))*g'(x)
f'(x) =
 *
*
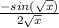 =
=