Question

Help pls!!!

y=3x+2 in standard and point-slope form
What are the points?
What is the slope?
What is the x-intercept
What is the y-intercept?
What is the parallel slope?
What is the perpendicular?

pls answer soon!!

Answer 1

Answer/Step-by-step explanation:

Standard Form:

`\[ -3x + y = 2 \]`

Point-Slope Form:

`\[ y - 2 = 3(x - 0) \]`

Points:

There are infinite points on this line. However, any pair of values for x and y that satisfy the equation forms a point on the line. For example, if
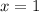`\(x = 1\)`, then
`\(y = 5\)`, so the point (1, 5) is on the line.

Slope:

The coefficient of x in the equation is the slope. In this case, the slope is 3.

X-intercept:

To find the x-intercept, set
`\(y = 0\)` and solve for x:

`\[ 3x + 2 = 0 \]`

`\[ 3x = -2 \]`

`\[ x = -(2)/(3) \]`

So, the x-intercept is
`\((-2/3, 0)\)`.

Y-intercept:

To find the y-intercept, set
`\(x = 0\)` and solve for y:

`\[ y = 3(0) + 2 \]`

`\[ y = 2 \]`

So, the y-intercept is
`\((0, 2)\)`.

Parallel Slope:

For a line parallel to this one, the slope would be the same, which is 3.

Perpendicular Slope:

For a line perpendicular to this one, the negative reciprocal of the slope is taken. The negative reciprocal of 3 is
`\(-(1)/(3)\)`. Therefore, a line perpendicular to the given line would have a slope of
`\(-(1)/(3)\)`.