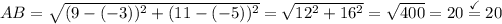Answer:
The midpoint is (3, 3).
Explanation:
We are given the two points A(9, 11) and B(-3, -5).
The midpoint is given by:
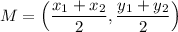
So:
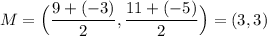
The midpoint is (3, 3).
We want to show that AM = MB.
We can use the distance formula:
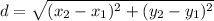
The distance between A(9, 11) and M(3, 3) will then be:
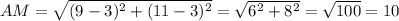
And the distance between B(-3, -5) and M(3, 3) will be:
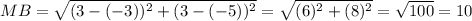
So, AM = MB = 10.
Since AM = MB = 10, AM + MB = 10 + 10 = 20.
So, we want to prove that AB = 20.
By the distance formula: