Question

A. In 2000, the population of a country was approximately 5.91 million and by 2077 it is projected to grow to 13 million. Use the exponential growth model A = A0e^kt, in which t is the number of years after 2000 and Ao is in millions, to find an exponential

growth function that models the data.

b. By which year will the population be 16 million?

Answer 1

a. k = 0.0072

b. 114 years

Explanation:

a. To find the exponential growth function, we can use the formula:

`A= A_oe^(kt)`

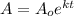
where:

• A is the final amount (population size at a given time)

• A0​ is the initial amount (initial population size)

• k is the rate of growth

• t is time

Given that A0​=5.91 million (the population in 2000), and A=13 million (the projected population in 2077), we can substitute these values into the equation. The time period, t, from 2000 to 2077 is 77 years. So, we get:

`13= 5.91e^(77k)`

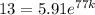
Solving this equation for k, we get:

`k = (1)/(77) ln((13)/(5.91) )`

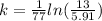
b. To find out by which year the population will be 16 million, we can substitute A=16, and solve for t:

`16 = 5.91e^(kt)`

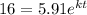
Solving this equation for t, we get:

`t= (1)/(k)ln((16)/(5.91) )`

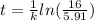
This will give us the number of years after 2000 when the population will reach 16 million.

a. Solving for k in the equation 13=5.91e^77k, we get:

`k= (1)/(77) ln((13)/(5.91) )= 0.0072`

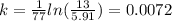
b. Substituting A=16 and k=0.0072 into the equation 16=5.91e^kt, and solving for t, we get:

`t = (1)/(0.0072)ln(16)/(5.91) = 114 \\`

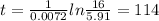
So, the population will reach 16 million approximately 114 years after 2000, which is around the year 2114.