Question

What is the equation of the line passing through the points (-25, 50) and (25, 50) in slope-interept form?

y = -50x
y = -50
y = 50x
y = 50

Answer 1

y = 50

Explanation:

The slope-intercept form of the equation of a line is:

y = mx + b

where:

• m is the slope of the line
• b is the y-intercept of the line

The slope of a line is a measure of its steepness. It is calculated using the following formula:

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

where:

`(x_1, y_1)` and
`(x_2, y_2)` are any two points on the line

The y-intercept of a line is the point where the line crosses the y-axis. It is equal to the value of y when x is equal to 0.

In this case, the two points given are (-25, 50) and (25, 50). The slope of the line is:

`\sf m = (50 - 50)/(25 - (-25)) \\\\ =( 0 )/( 50) \\\\ = 0`

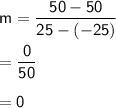
The y-intercept of the line is 50, since the line passes through the point (0, 50).

Therefore, the equation of the line in slope-intercept form is:

y = 0x + 50

or simply:

y = 50

This is because the slope of the line is 0, which means that the line is horizontal and does not change in value as `x` changes.

Therefore, the value of y is always equal to 50.

So, the answer is:

y = 50