Question

This makes no sense I need help asap

Answer 1

x = 15°

m ∠1 = 115°

m ∠2 = 65°

Explanation:

Alternate angles are two non-adjacent interior angles that lie on opposite sides of a transversal and are intersected by two parallel lines. Alternate angles are congruent.

In this case:

(x+50)° and (3x + 20)° are alternate angles.

So,

(x + 50)° = (3x + 20)°

x + 50 = 3x + 20

Subtract 20 on both sides:

x + 50 - 20 = 3x + 20 - 20

x + 30 = 3x

Subtract x on both sides:

x + 30 - x = 3x - x

30 = 2x

Divide both sides by 2.

`\sf (30)/(2)=(2x)/(2)`

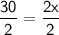
15 = x

Therefore,

x = 15

Again

Corresponding angles are two angles that lie on the same side of a transversal and are intersected by two parallel lines. Corresponding angles are congruent.

In this case:

m ∠2 and (3x + 20)° are corresponding angles.

So,

m∠2 = (3x + 20)°

Substitute the value of x.

m ∠2 = (3×15 + 20)°

m ∠2 = (45+20)°

m ∠2 = 65°

And

A linear pair is two adjacent angles that form a straight line. The sum of the measures of the angles in a linear pair is 180 degrees.

In this case:

m ∠1 and (3x + 20)° are linear pair and the angles are supplementary.

So,

m∠1 + (3x + 20)° = 180°

Substitute the value of x.

m ∠1 + (3×15 + 20)° = 180°

m ∠1 + (45 + 20)° = 180°

m ∠1 + 65° = 180°

Subtract 65° on both sides:

m ∠1 + 65° - 65° = 180° - 65°

m ∠1 = 115°

Therefore,

• x = 15°
• m ∠1 = 115°
• m ∠2 = 65°

Answer 2

x = 15 , ∠ 1 = 115° , ∠ 2 = 65°

Explanation:

the figure has opposite sides parallel

the figure is therefore a parallelogram

(3x + 20 )° and (x + 50)° are alternate angles and are congruent (equal) , so

3x + 20 = x + 50 ( subtract x from both sides )

2x + 20 = 50 ( subtract 20 from both sides )

2x = 30 ( divide both sides by 2 )

x = 15

Then

x + 50 = 15 + 50 = 65°

• consecutive angles of a parallelogram are supplementary ( sum to 180° )

∠ 1 and (x + 50)° are consecutive angles , that is

∠ 1 + 65° = 180° ( subtract 65° from both sides )

∠ 1 = 115°

• opposite angles of a parallelogram are congruent , then

∠ 2 = (x + 50)° = 65°