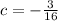Answer:
Explanation:
First of all, I'm assuming we're finding c and not e.
Anyway, the inflection point is found where the second derivative is equal to 0. Therefore, if
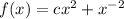 , then
, then
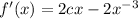 and
and
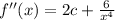
Now we'll evaluate that at an x value of 2, set the whole thing equal to 0, and solve for c:
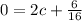 which simplifies to
which simplifies to
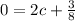 and
and
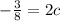 so
so