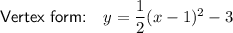Question

Please help fast!!! Need this answer to move on!

sketch the graph. write the domain and range

Answer 1

Vertex form of parabola

• y =a(x-h)²+k

where (h,k) is vertex

here it's upward facing parabola so a is positive

• vertex at (1,-3)

Now equation

• y=a(x-1)²-3

We need a now

Find a point let it be (3,-1)

Put in equation

• -1=a(3-1)²-3
• 2=4a
• a=1/2

Let's verify once

• y=1/2(x-1)²-3

Put (-1,-1)

• -1=1/2(-2)²-3
• 2=1/2(4)
• 2=2

Verified

Now

the equation is

• y=1/2(x-1)²-3

Domain:

• Domain is set of x values

Here x can be any real no

• So domain is R

Range:

• Range is set of y values

Put x=1 for maximum value[ because (x-1)² is always +ve]

• y=-3

So range

• [-3,oo)

Answer 2

Domain: (-∞, ∞)

Range: [-3, ∞)

Explanation:

Domain

The domain of a function is the set of all possible input values (x-values) for which the function is defined.

A quadratic function, represented by a parabola with a vertical axis of symmetry, has a domain that includes all real values of x, meaning it is defined for all values of x. The given graph shows an upward-opening parabola. Therefore, the domain of the graph is (-∞, ∞).

Range

The range of a function is the set of all possible output values (y-values) for which the function is defined.

The range of an upward-opening parabola is all real numbers greater than or equal to the y-coordinate of the vertex. The vertex of an upward-opening parabola is the point where the parabola reaches its minimum value (lowest point). From observation of the given graph, the y-coordinate of the vertex is y = -3. Therefore, the range of the graph is [-3, ∞).

`\hrulefill`

Additional Notes

Note that the equation of the graphed parabola is:

`\textsf{Vertex form:} \quad y=(1)/(2)(x-1)^2-3`

`\textsf{Standard form:} \quad y=(1)/(2)x^2-x-(5)/(2)`