Question

b) If the half-life of a radioactive substance is 5 days, how long will it take for a 100 gram sample to decay to one-eighth its original mass? [2]

Answer 1

It takes 15 days for a 100 gram sample of a radioactive substance with a half-life of 5 days to decay to one-eighth of its original mass, going through three half-life cycles.

Step-by-step explanation:

If the half-life of a radioactive substance is 5 days, to determine how long it will take for a 100 gram sample to decay to one-eighth of its original mass, we need to recall that each half-life period reduces the substance’s quantity by half. Here’s how it breaks down:

• After one half-life (5 days), 50 grams remain.
• After two half-lives (10 days), 25 grams remain.
• After three half-lives (15 days), 12.5 grams remain.

Therefore, it would take 15 days for a 100 gram sample to decay to one-eighth (12.5 grams) of its original mass.

Answer 2

It will take 15 days for a 100 gram sample to decay to one-eighth its original mass.

To calculate the time it will take for a 100-gram sample of a radioactive substance to decay to one-eighth its original mass, given its half-life is 5 days, we'll use the formula for exponential decay.

The formula is:

`\[ N = N_0 * \left( (1)/(2) \right)^{(t)/(T)} \]`

Where:

-
`\( N \)` is the final amount of the substance.

-
`\( N_0 \)` is the initial amount of the substance.

-
`\( t \)` is the time period.

-
`\( T \)` is the half-life of the substance.

In this case, we want to find
`\( t \) when \( N = (N_0)/(8) \) and \( T = 5 \) days.`

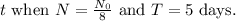
Step 1: Set up the equation with the given values:

`\[ (N_0)/(8) = N_0 * \left( (1)/(2) \right)^{(t)/(5)} \]`

Step 2: Simplify the equation. Since
`\( N_0 \)` is on both sides, we can cancel it out:

`\[ (1)/(8) = \left( (1)/(2) \right)^{(t)/(5)} \]`

Step 3: Solve for \( t \). This involves using logarithms. First, we can rewrite the equation as:

`\[ 2^(-3) = 2^{(-t)/(5)} \]`

Thus,
`\(-3 = (-t)/(5)\)`

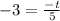
Step 4: Multiply both sides of the equation by -5 to isolate
`\( t \)`:

`\[ t = 3 * 5 \]`

Step 5: Calculate the value of
`\( t \)`:

`\[ t = 15 \]`

So, it will take 15 days for a 100 gram sample to decay to one-eighth its original mass.