Question

Sketch the graph of each function. Then State the domain, range and increasing, decreasing intervals. Part 1​

Answer 1

Problem 15

Answers:

• Graph: Shown below
• Domain: [3, infinity)
• Range: [2, infinity)
• Increasing interval: [2, infinity)
• Decreasing interval: None

Each interval is interval notation.

----------------------------------

Step-by-step explanation:

To get the graph, you can plug in various x values to find their paired y values, then draw a curve through those points. You can only plug in x values that are 3 or larger, as I'll mention later in the next paragraph. A quicker way to get the graph is to use technology. I used GeoGebra to generate the graphs below.

To get the domain, we need to ensure that the stuff under the square root is never negative. So we need to make the x-3 to be 0 or larger. Solving
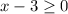`x-3 \ge 0` leads to
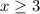`x \ge 3` showing that 3 is the smallest value we can plug in. The domain is the interval from 3 to positive infinity. We can write that as
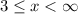`3 \le x < \infty` which condenses to the interval notation [3, infinity). Note how the square bracket is used to include the endpoint.

The range can be determined from the graph. The lowest point is when y = 2, so the range consists of y outputs that are 2 or larger. We write the interval notation [2, infinity) to mean
`2 \le y < \infty`

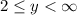
The graph also helps us see where the curve is increasing or decreasing. In this case, the curve goes uphill as we move from left to right. Therefore, the graph is increasing over its entire domain. We write the domain as the answer here. Because the function increases over the entire domain, there's no room for the function to decrease.

===========================================================

Problem 16

Answers:

• Graph: Shown below
• Domain: [-1, infinity)
• Range: [-3, infinity)
• Increasing interval: [-1, infinity)
• Decreasing interval: None

----------------------------------

Step-by-step explanation:

We follow the same idea as the previous problem.

This time we want the x+1 under the square root to be 0 or larger, so
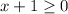`x+1 \ge 0` solves to
`x \ge -1` telling us the smallest input allowed. The value of x can be this or larger.

Since this is an increasing function throughout the domain (similar to the previous problem), this means that the smallest domain value corresponds exactly to the smallest range value. Plugging in x = -1 leads to y = -3 which is the smallest possible output. As x gets bigger, so does y. The graph shows that the lowest point occurs when y = -3 to visually confirm this.

The increasing interval is over the entire domain, so we just write the domain again for the increasing interval. This means we write "none" for the decreasing interval.

Side note: The graphs are shown together on the same xy coordinate axis, but for your hw problem, you'll have the graphs on their own separate grid.