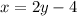Question

Y= 1/2x+ 2 to make the x the subject.

Answer 1

`x=2y-4`

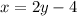
Explanation:

`y=(1)/(2) x+2`

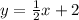
"To make x the subject" means to have the equation with all the terms in x on one side. As of now, y is the subject of the equation.

You start by subtracting 2 from both sides, you should get the following.

`y-2=(1)/(2) x`

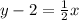
Then you multiply by 2 from both sides, you should end up with the following.

`2(y-2)=x`

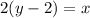
Therefore, you get the following.

`x=2(y-2)`

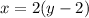
Finally, you distribute and get the answer.

`x=2y-4`