Answer:
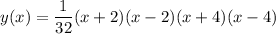
Explanation:
The root of a polynomial is a point on the graph where the curve intersects or crosses the x-axis, meaning that the function equals zero at that point.
From observation of the given graph, the roots of the polynomial are:
The curve exhibits symmetry about the y-axis.
According to the Factor Theorem, if a polynomial f(x) has a root at x = a, then (x - a) is a factor of f(x).
The multiplicity of a root refers to the number of times the associated factor appears in the factored form of the equation of a polynomial.
When a root has a multiplicity of one, the graph of the polynomial function crosses the x-axis at that particular value of x. The concavity of the graph remains the same as it approaches and passes through the x-axis. Therefore, all roots of the graphed function have multiplicity one.
So, a possible factored form of the graphed function is:
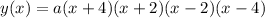
where 'a' is the leading coefficient.
The y-intercept is the point on the graph where the curve intersects the y-axis. Therefore, the y-intercept is at (0, 2).
To find the leading coefficient (a), we can substitute (0, 2) into the function and solve for a:
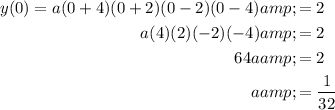
So, the equation of the graphed function in factored form is:
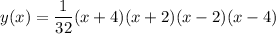
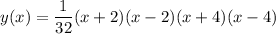
This equation satisfies the observed characteristics of the graph.