Question

In of a factory, There are 100 units of a certain product, 5 of which are defective. if 3 units are selected from The 100 units at random, then What is the probability that none of them are defective.

Answer 1

`\bold{ANSWER:}`
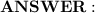
0.0781 or 7.81%


`\bold{SOLUTION:}`

To find the probability that none of the selected units are defective, we need to calculate the ratio of the number of favorable outcomes (selecting 3 non- defective units) to the total number of possible outcomes (selecting any 3 units).

The total number of possible outcomes can be calculated using the combination formula: nCr = n! / (r!(n-r)!), where n is the total number of units and r is the number of units selected.

In this case, n = 100 (total number of units) and r (number of units selected). So the total number of possible outcomes is:

100C3 = 100! / (3!(100-3)!) = (100 * 99 * 98) / (3 * 2 * 1) = 161,700

Now, let's calculate the number of favorable outcomes, which is selecting 3 non-defective units. Since there are 5 defective units, we need to choose 3 units from the remaining 100 - 5 = 95 units.

95C3 = 95! / (3!(95-3)!) = (95 * 94 * 93) / (3 * 2 * 1) = 12,650

Therefore, the probability that none of the selected units are defective is:

P(None defective) = favorable outcomes / total outcomes = 12,650 / 161,700 ≈ 0.0781

So, the probability is approximately 0.0781 or 7.81%