Answer:
The zeroes of this polynomial are
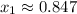 and
and
 .
.
Explanation:
Let
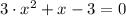 , the quickest and most efficient approach to find the zeroes of this second order polynomial is by Quadratic Formula. For all
, the quickest and most efficient approach to find the zeroes of this second order polynomial is by Quadratic Formula. For all
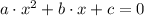 , roots are determined by:
, roots are determined by:
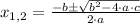 (1)
(1)
Where
 ,
,
 ,
,
 are coefficients of the polynomial.
are coefficients of the polynomial.
If we know that
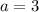 ,
,
 and
and
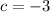 , then roots of the polynomial are, respectively:
, then roots of the polynomial are, respectively:
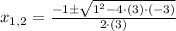
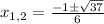
The zeroes of this polynomial are
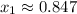 and
and
 .
.