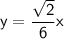Question

18y^2-x^2=18.

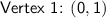
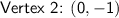
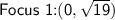
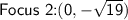
Identify the vertices, foci, and the equations of the asymptotes of the hyperbola

There should be 2 vertices, 2 foci, and 2 asymptote equations

Answer 1

`\textsf{Center:}\quad (0, 0)`

`\textsf{Vertices:}\quad (0, -1)\; \textsf{and}\;(0,1)`

`\textsf{Foci:}\quad \left(0,-√(19)\right) \;\;\text{and}\;\;\left(0,√(19)\right)`

`\textsf{Asymptotes:} \quad y= (√(2))/(6)x\;,\quad y=- (√(2))/(6)x`

Explanation:

Given equation of the hyperbola:

`18y^2-x^2=18`

Since the y-term is positive, the hyperbola is vertical and opens up and down.

The standard equation of a vertical hyperbola is:

`\boxed{\begin{minipage}{7.4 cm}\underline{Standard equation of a vertical hyperbola}\\\\$((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center. \\ \phantom{ww}$\bullet$ $(h, k\pm a)$ are the vertices. \\\phantom{ww}$\bullet$ $(h\pm b, k)$ are the co-vertices. \\\phantom{ww}$\bullet$ $(h, k\pm c)$ are the foci where $c^2=a^2+b^2$\\\phantom{ww}$\bullet$ $y =k \pm \left((a)/(b)\right)(x-h)$ are the asymptotes.\\\end{minipage}}`

First, rearrange the equation to the standard form of a hyperbola:

`\begin{aligned}18y^2-x^2&=18\\\\(18y^2)/(18)-(x^2)/(18)&=(18)/(18)\\\\y^2-(x^2)/(18)&=1\end{aligned}`

Therefore, the values of h, k, a² and b² are:

• 
  `h = 0`
• 
  `k =0`
• 
  `a^2 = 1 \implies a=√(1)=1`
• 
  `b^2 = 18 \implies b=√(18)=3√(2)`

So, the center (h, k) of the hyperbola is located at the origin (0, 0).

To find the coordinates of the vertices, substitute the values of h, k and a into the vertices formula:

`\begin{aligned}\textsf{Vertices}&=(h, k \pm a)\\&=(0, 0 \pm 1)\\&=(0, -1)\; \textsf{and}\;(0,1)\end{aligned}`

To find the foci, we first need to find the value of c by substituting the values of a² and b² into the equation c² = a² + b²:

`\begin{aligned}c^2&=a^2+b^2\\c&=√(a^2+b^2)\\c&=√(1+18)\\c&=√(19)\end{aligned}`

Now, to determine the foci, substitute the values of h, k and c into the foci formula:

`\begin{aligned}\sf Foci&=(h,k\pm c)\\&=\left(0,0\pm √(19)\right)\\&=\left(0,\pm √(19)\right)\end{aligned}`

To find the equations of the asymptotes, substitute the values of h, k, a and b into the asymptote formula:

`\begin{aligned}y&=k \pm \left((a)/(b)\right)(x-h)\\\\y&=0 \pm \left((1)/(3√(2))\right)(x-0)\\\\y&= \pm (1)/(3√(2))x\\\\y&= \pm (√(2))/(3√(2)√(2))x\\\\y&= \pm (√(2))/(6)x\end{aligned}`

Therefore, the equations of the asymptotes are:

`y= (√(2))/(6)x`

`y= -(√(2))/(6)x`

Answer 2

Vertices:

`\sf \textsf{Vertex 1: } (0,1)`

`\sf \textsf{Vertex 2: } (0, -1 )`

Foci:

`\sf \textsf{Focus 1:} (0, √(19))`

`\sf \textsf{Focus 2:} (0,- √(19))`

Equations of the asymptotes:

`\sf y = (√(2))/(6)x`

`\sf y = - (√(2))/(6)x`

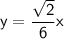
Explanation:

`\sf 18y^2-x^2=18`

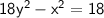
The given equation, represents a hyperbola. To identify its vertices, foci, and equations of asymptotes, we first need to rewrite the equation in standard form, which is of the form:

For a horizontal hyperbola

`\sf ((x - h)^2 )/( a^2) - ((y - k)^2 )/(b^2) = 1`

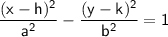
For a vertical hyperbola

`\sf ((y - k)^2 )/( b^2) - ((x - h)^2 )/(a^2) = 1`

Where:

• (h, k) is the center of the hyperbola.
• 'a' is the distance from the center to the vertices along the major axis.
• 'b' is the distance from the center to the co-vertices along the minor axis.

In this case, let's rewrite the given equation:

`\sf 18y^2-x^2=18`

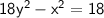
Divide the equation by 18 to get it in the standard form:

`\sf (y^2 )/(1) -(x^2 )/( 18) = 1`

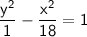
Comparing the coefficients with standard form for a vertical hyperbola. we have:

• h = 0 (since there's no x-term in the equation, the x-coordinate of the center is 0).
• k = 0 (since there's no constant on the right side of the equation, the y-coordinate of the center is 0).
• a^2 = 18 (from the coefficient of the x^2 term).
• b^2 = 1 (from the coefficient of the y^2 term).

Now that we have the values of 'h', 'k', 'a', and 'b', we can find the vertices, foci, and equations of the asymptotes.

Vertices:

The vertices are located along the major axis. For a vertical hyperbola, the vertices are given by (h , k ± b), which in this case are:

`\sf ( 0, 0 \pm 1 )`

`\sf ( 0, \pm 1)`

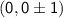
So the vertices are:

`\sf \textsf{Vertex 1: } (0,1)`

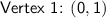
[tex]\sf \textsf{Vertex 2: } (0, -1 ) [/tex]

Foci:

The distance from the center to the foci is given by c, where

`\sf c^2 = a^2 + b^2`

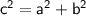
In this case,

`\sf c^2 = 18 + 1`

`\sf c^2 = 19`

`\sf c = √(19)`

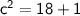
The foci are located along the minor axis, so their coordinates are (h , k ± c):

`\sf (0, 0\pm √(19))`

`\sf (0,\pm √(19))`

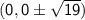
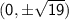
So,

`\sf \textsf{Focus 1:} (0, √(19))`

`\sf \textsf{Focus 2:} (0,- √(19))`

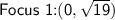
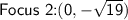
Equations of Asymptotes:

The equations of the asymptotes for a vertical hyperbola are given by:

`y = \pm (b)/(a)(x - h) + k`

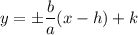
Substituting the value, we get

`\sf y = \pm (1)/(√(18))(x - 0) + 0`

`\sf y = \pm (1)/(√(18))x`

`\sf y = \pm (1)/(3√(2))x`

`\sf y = \pm (1)/(3√(2))x * (√(2))/(√(2))`

`\sf y = \pm (√(2))/(3* 2)x`

`\sf y = \pm (√(2))/(6)x`

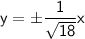
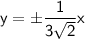
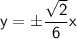
So, the equations of the asymptotes are:

`\sf y = (√(2))/(6)x`

`\sf y = - (√(2))/(6)x`