The cosine sum identity is:
![\[ \cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6hory6d56mffgl5a4zilwqkcjv3ixilo5h.png)
This is the cosine double-angle identity in its first form.
![\[ \cos(2A) = \cos^2(A) - \sin^2(A) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1dy56sw5jlmavdyyq1qhlrfis99hf3vgk3.png)
To derive the cosine double-angle identity using the cosine sum identity, we start with the known sum identity for cosine and then apply it to the specific case of a double angle. The cosine sum identity is:
![\[ \cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6hory6d56mffgl5a4zilwqkcjv3ixilo5h.png)
The cosine double-angle identity we want to prove is one of the following forms:
1.
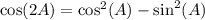
2.
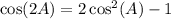
3.
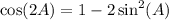
Let's prove the first form and then show how it can lead to the other two forms.
Step 1: Apply the Cosine Sum Identity to a Double Angle
Let's set A = B in the cosine sum identity:
![\[ \cos(A + A) = \cos(A)\cos(A) - \sin(A)\sin(A) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jdmhvsmt3puqovf2f2x36r97sgk1e5k4bv.png)
![\[ \cos(2A) = \cos^2(A) - \sin^2(A) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1dy56sw5jlmavdyyq1qhlrfis99hf3vgk3.png)
This is the cosine double-angle identity in its first form.
Step 2: Derive the Other Forms
1. To derive the second form, use the Pythagorean identity
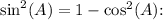
![\[ \cos(2A) = \cos^2(A) - (1 - \cos^2(A)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/icl3b6l3pc9d4hzp7q9spidq21t9a2n0e5.png)
![\[ \cos(2A) = 2\cos^2(A) - 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xhwqutrdmmtixdomkz2id0se0rbkla4d0w.png)
2. To derive the third form, use the Pythagorean identity
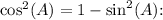
![\[ \cos(2A) = (1 - \sin^2(A)) - \sin^2(A) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v4e1vcfex9x2kwv6tarkjvy8rf07t7aw6n.png)
![\[ \cos(2A) = 1 - 2\sin^2(A) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ulfuc52gjqvjtqploeq353juyjyyih0yt5.png)
Conclusion
Thus, we have derived the cosine double-angle identity from the cosine sum identity and also shown how it can be expressed in multiple forms.