Question

Find

f ∘ g ∘ h.

`f(x) = (1)/(x) , g(x) = x^3, h(x) = x^2 + 5`

(just a little confused on what to do for composite fractions)

Answer 1

1/(x^2+5)^3 *

Explanation:

Answer 2

`\sf (f\circ g\circ h)(x) = (1)/( (x^2+5)^3)`

Explanation:

Given:

`\sf f(x) = (1)/(x)`

`\sf g(x) = x^3`

`\sf h(x) = x^2 + 5`

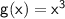
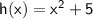
To find:

`\sf f\circ g \circ h`

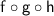
Definition:

Solution:

Given:

`\sf f(x) = (1)/(x)`

`\sf g(x) = x^3`

`\sf h(x) = x^2 + 5`

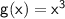
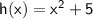
To find:

`\sf f\circ g \circ h`

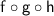
Definition:

The composite function
`\sf fcirc g\circ h` is defined as follows:

`\sf (f\circ g\circ h)(x) = f(g(h(x)))`

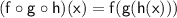
In other words, to evaluate
`\sf f\circ g\circ h` at a point x, we first evaluate h(x), then substitute that result into g(x), and finally substitute the result of that into f(x).

Solution:

To find
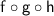`\sf f\circ g \circ h`, we simply substitute the functions $g(x)$ and $h(x)$ into the function $f(x)$ as follows:

`\sf \begin{aligned} f\circ g\circ h(x) & = f(g(h(x))) \\\\ &= f(g(x^2+5))\\\\ &= f((x^2 + 5)^3 )\\\\ &= (1)/( (x^2+5)^3) \end{aligned}`

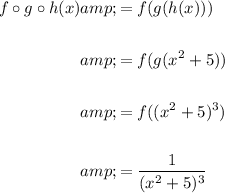
Therefore,

`\sf (f\circ g\circ h)(x) = (1)/( (x^2+5)^3)`