Given f(x)=x^3-2, find the equation of the secant line passing through (-4,f(-4)) and (2,f(2))

Question

asked Sep 4, 2022 217k views

1 Answer

Cjk · Answer 1 · 2022-09-11T14:28:02+0000

Given:

The function is

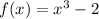
f(x)=x^3-2

The secant line passing through (-4,f(-4)) and (2,f(2)).

To find:

The equation of the secant line.

Solution:

We have,

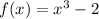
f(x)=x^3-2

At x=-4,

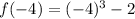
f(-4)=(-4)^3-2

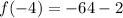
f(-4)=-64-2

f(-4)=-66

At x=2,

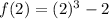
f(2)=(2)^3-2

f(2)=8-2

f(2)=6

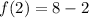
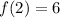
The secant line passes through the points (-4,-66) and (2,6). So, the equation of the secant line is

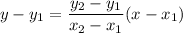
y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)

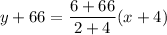
y-(-66)=(6-(-66))/(2-(-4))(x-(-4))

y+66=(6+66)/(2+4)(x+4)

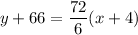
y+66=(72)/(6)(x+4)

On further simplification, we get

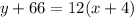
y+66=12(x+4)

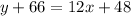
y+66=12x+48

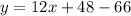
y=12x+48-66

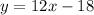
y=12x-18

Therefor, the equation of the secant line is
.
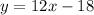