Answer:
Explanation:
Hi there!
The given geometric sequence is: 2,-4,8.....
Then,
1st term = 3
Common ratio = t2/t1
= -4/2
= -2
We have,
General term of geometric sequence = a*
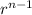
Where "n" is no. of terms
an = a*
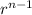
or, a12 = 2*
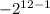
= 2*-2048
= -4096
Therefore, the 12th term is -4096.
Hope it helps!