Question

Write an exponential function that passes through (0,3) and (1,6). Write your answer in the form f(x) = ab^x

Answer 1

`\boxed{f(x)=(3)(2)^x}`

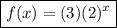
Explanation:

First, we need to substitute the coordinates of the two given points in the ecuation
`f(x)=ab^x`:

`3=ab^(0) \qquad \textbf{ec.1}\\6=ab^(1) \qquad \textbf{ec.2}`

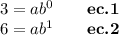
Remember that any number raised to the power 0 is equal to 1. So:

`3=a \qquad \textbf{ec.3}`

now, we can substitute in ec.2 and solve for b:

`6=3b\\ b=2`

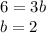
Finally:

`f(x)=(3)(2)^x`

Therefore, we have found the solution to the exercise

`\text{-B$\mathfrak{randon}$VN}`