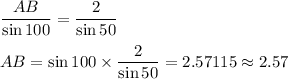Question

Instructions Use this triangle for problems 1-3

1. what is the value of angle B?

2. What is the length of BC

3. What is the length of AB​

Answer 1

Q1 Value of angle B = 50°

Q2 BC = 1.3

Q3 AB = 2.57

Explanation:

For Part 1
The three angles of a triangle must add up to 180°

Therefore m∠B + 30 + 100 = 180

m∠B + 130 = 180

m∠B = 180 - 30 = 50°

part 2
The law of sines states that, in a triangle, the ratio of each side to the sine of the angle opposite that side must be the same for all sides

We have side AC opposite ∠B

AC = 2 and we found that m∠B = 50° from part 1

The side BC is opposite ∠A which is 30°

Therefore, applying the law of sines

`\frac{{AC}}{\sin 50^\circ} = \frac{{BC}}{\sin 30^\circ}\\\\\\(2)/(\sin 50^\circ) = \frac{{BC}}{\sin 30^\circ}\\\\`

Multiplying both sides by sin 30° we get

`(2)/(\sin 50^\circ) * \sin 30^\circ =BC\\\\or\\\\BC = (2)/(\sin 50^\circ) * \sin 30^\circ`

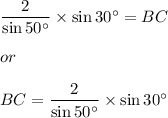
Using a calculator to compute the right side we get
BC = 1.30540 ≈ 1.3

part 3

Similarly

`(AB)/(\sin 100) = (2)/(\sin50)\\\\AB = \sin 100 * (2)/(\sin 50) = 2.57115 \approx 2.57`