Answer:
each of the other sides is 2√2 = 2.8284
Explanation:
A 45°- 45°-90° triangle is also known as a right isosceles triangle because two of the legs are the same as two of the angles are the same at 45°
If a is the length of one of the legs then the hypotenuse, h, which is the longest side is given by the equation

Or, dividing by √2 on both sides,
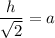
Given h = 4
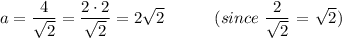
a = 2√2 = 2.8284
So each of the other sides is 2√2 = 2.8284